مهدی حسین پورمقدمی
دبیر ریاضی ، تبریز
مهدی حسین پورمقدمی
دبیر ریاضی ، تبریزدرباره من
پر بازدیدها
سوالات نهایی دوازدهم ریاضی مهدی حسین پورمقدمی سوالات نهایی دوازدهم ریاضیات نهم مهدی مقدمی سوالات نهایی دوازدهم انسانی ریاضی و آمار (3) حسابان 2 ریاضی نهم استدلال عقلانی شهریور 1402 سوالات ریاضی هماهنگ استان آذربای ریاضیات نهم نهایی ریاضی نهم تضمینی riazyamoz سوالات نهایی دوازدهم تجربی دوازدهم ریاضی ریاضیات گسسته نهایی دوازدهم ریاضی و آمار 3 خرداد99 ریاضی و آمار (3) دوازدهم انسانی دوازدهم انسانی ریاضی 3 دوازدهم تجربی تبریزجدیدترین یادداشتها
همه- بارم بندی امتحان ریاضی نهم
- بارم بندی ریاضی پایه هشتم
- آموزش آنلاین ریاضیات
- نمونه سوال ریاضی هشتم فصلهای 1 تا 5
- شروع به فعالیت کانال در آپارات
- شروع کلاسهای آمادگی برای امتحانات خرداد
- آزمون ورودی پایه دهم مدارس نمونه دولتی استان آذربایجان شرقی
- آزمون آنلاین ریاضی نهم
- عیدتان مبارک دانش اموزان عزیز
- شروع کلاسهای آموزشی ریاضی
بایگانی
- فروردین 1404 6
- فروردین 1403 3
- اسفند 1402 1
- دی 1402 1
- آذر 1402 37
- آبان 1402 1
- مهر 1402 15
- شهریور 1402 18
- مرداد 1402 11
- تیر 1402 3
- خرداد 1402 3
- اردیبهشت 1402 1
- فروردین 1402 3
- دی 1401 10
- آبان 1401 1
- مرداد 1401 2
- خرداد 1401 2
- فروردین 1401 3
- بهمن 1400 2
- دی 1400 1
- آذر 1400 1
- آبان 1400 3
- شهریور 1400 2
- مرداد 1400 2
- اسفند 1399 1
- بهمن 1399 3
- دی 1399 4
- آذر 1399 2
- آبان 1399 8
- شهریور 1399 3
- مرداد 1399 3
- تیر 1399 9
- خرداد 1399 3
- فروردین 1399 1
- بهمن 1398 5
- دی 1398 1
- آبان 1398 4
- شهریور 1398 30
- مرداد 1398 5
- آذر 1397 4
- خرداد 1397 1
- اردیبهشت 1397 5
- فروردین 1397 2
تقویم
فروردین 1404| ش | ی | د | س | چ | پ | ج |
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
جستجو
عدد پی
عدد پی
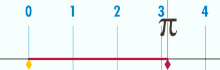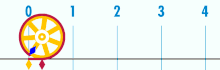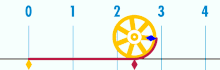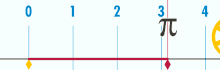
عدد پی (۳٫۱۴۱۵ = π) از اعداد گنگ است. عدد پی در بسیاری از معادلاتی که با نوسان و تناوب سر و کار دارند ظاهر میشود. بنا به شواهد تاریخی نخستین بار عدد پی توسط بابلیان (۳٫۱۲۵) و مصریان (۳٫۱۶۰۴) در ۱۹۰۰ سال قبل از میلاد محاسبه شد که هر دو تا یک رقم اعشار صحیح است. همچنین در متون هندی این عدد ۳٫۱۳۹ تقریب زده شده که حدوداً تا دو رقم اعشار صحیح است. اولین کسی که عدد پی را با دقت قابل قبول تخمین زد، ارشمیدس در قرن سه قبل از میلاد بود. او به کمک روش تقریب دایره با چند ضلعیهای منتظم و به کمک ۹۶ ضلعی منتظم عدد پی را ۳٫۱۴۱۹ تخمین زد که تا سه رقم اعشار صحیح است. همچنین دانشمندی چینی بنام زو چانگ ژی در قرن ۵ میلادی عدد پی را ۳٫۱۴۱۵۹۲۹۲ محاسبه کرد که تا ۶ رقم اعشار صحیح است. غیاث الدین جمشید کاشانی دانشمند و ریاضی دان ایرانی نیز عدد پی را تا 17 رقم اعشار بدست آورد که تنها در رقم هفدهم با محاسبات امروزی تفاوت داشت. تا هزاره دوم میلادی کمتر از ده رقم اعشار عدد پی بهطور صحیح محاسبه شده بود (به کمک عدد پی تا ۱۱ رقم اعشار میتوان محیط کره زمین را با دقت میلیمتر تخمین زد). رفته رفته و با پیشرفت ریاضیات و ابداع روش سریهای نامتناهی تخمینهای بهتر و بهتری برای عدد پی بدست آمد، بطوریکه امروزه با استفاده از رایانههای شخصی میتوان این عدد را تا میلیاردها رقم اعشار صحیح تخمین زد. اگر میخواهید عدد p را تا ده رقم اعشار به خاطر بسپارید تعداد حروف کلماتِ این شعر به شما کمک خواهد کرد:
خرد و بینش و آگاهی دانشمندان ره سرمنزل مقصود بما آموزد= ۳/۱۴۱۵۹۲۶۵۳۵