پروژه ای برای شکار اعداد اول بزرگ

کشف طولانی‌ترین عدد اول با 23 میلیون رقم

تلاش محاسباتی مشترک ریاضیدانان به کشف طولانی‌ترین عدد اول منجر شد.

تلاش محاسباتی مشترک ریاضیدانان به کشف طولانی ترین عدد اول منجر شد.این رقم جدید که بیش از 23 میلیون رقم دارد، به اختصار M77232917 نامیده شده است.
اعداد اول تنها بر خود و عدد یک قابل تقسیم هستند و جستجو برای کشف اعداد اولی که همواره بزرگتر باشند، از مدت ها قبل علاقمندان به ریاضی را به خود مشغول کرده است.
با این وجود، این قبیل تحقیقات به نرم افزارهای پیشرفته و همکاری محققان نیاز دارد زیرا کشف این اعداد بسیار دشوار است.
عدد M77232917 در کامپیوتر 'جاناتان پیس' یک مهندس برق در امریکا محاسبه شد که از 14 سال قبل در جستجوی کشف اعداد اول بزرگ است.
وی این عدد اول را در بخشی از 'تحقیق اینترنتی بزرگ عدد مرسن' (GIMPS) کشف کرد؛ پروژه ای که سال 1996 برای شکار اعداد اول بزرگ آغاز شد.
اعداد مرسن از مضرب اعداد بسیاری در مبنای دو و سپس منهای یک محاسبه می شود.
شش روز محاسبه بی وقفه که در آن اعداد 77,232,917 در مبنای دو در هم ضرب شدند، به کشف بزرگترین عدد اول شناخته شده تاکنون، منجر شد.
این عدد پنجاهمین عدد مرسن و شانزدهمین عدد اولی است که در جریان پروژه GIMPSکشف شده است.
این عدد تقریبا یک میلیون رقم طولانی تر از عدد اول رکوردار قبلی است که در اوایل سال 2016 در بخشی از همین پروژه کشف شد.
با این وجود، تازه ترین عدد اول بزرگ کشف شده باید با استفاده از چهار برنامه مختلف رایانه ای در چهار کامپیوتر مختلف بررسی شود.
پیس به دلیل این کشف، جایزه 3 هزار دلاری (2.211 یورویی) تحقیق GIMPS را دریافت خواهد کرد.
کشف عدد مرسن بعدی می تواند کوتاه تر یا بلندتر از عدد مرسن رکورد دار موجود باشد اما هدف بزرگ گروه GIMPS کشف یک عدد اول با 100 میلیون رقم است.

منبع : ایرنا

فهرست هزار عدد اول

عدد اول (به انگلیسی: Prime Number)، عددی طبیعی بزرگ‌تر از ۱ است که نتوان آن را به‌صورت ضرب دو عدد طبیعی کوچک‌تر نوشت (یعنی یکی از آن‌ها نمی‌تواند با خود عدد برابر باشد). به عبارت ساده‌تر، اعداد اول، مجموعه‌ای از اعداد طبیعی بزرگ‌تر از ۱ هستند که فقط بر یک و خود عدد بخش‌پذیر هستند.

منبع : لینک

فهرست هزار عدد اول[ویرایش]

ردیف	۱	۲	۳	۴	۵	۶	۷	۸	۹	۱۰	۱۱	۱۲	۱۳	۱۴	۱۵	۱۶	۱۷	۱۸	۱۹	۲۰
۱–۲۰	۲	۳	۵	۷	۱۱	۱۳	۱۷	۱۹	۲۳	۲۹	۳۱	۳۷	۴۱	۴۳	۴۷	۵۳	۵۹	۶۱]	۶۷	۷۱
۲۱–۴۰	۷۳	۷۹	۸۳	۸۹	۹۷	۱۰۱	۱۰۳	۱۰۷	۱۰۹	۱۱۳	۱۲۷	۱۳۱	۱۳۷	۱۳۹	۱۴۹	۱۵۱	۱۵۷	۱۶۳	۱۶۷	۱۷۳
۴۱–۶۰	۱۷۹	۱۸۱	۱۹۱	۱۹۳	۱۹۷	۱۹۹	۲۱۱	۲۲۳	۲۲۷	۲۲۹	۲۳۳	۲۳۹	۲۴۱	۲۵۱	۲۵۷	۲۶۳	۲۶۹	۲۷۱	۲۷۷	۲۸۱
۶۱–۸۰	۲۸۳	۲۹۳	۳۰۷	۳۱۱	۳۱۳	۳۱۷	۳۳۱	۳۳۷	۳۴۷	۳۴۹	۳۵۳	۳۵۹	۳۶۷	۳۷۳	۳۷۹	۳۸۳	۳۸۹	۳۹۷	۴۰۱	۴۰۹
۸۱–۱۰۰	۴۱۹	۴۲۱	۴۳۱	۴۳۳	۴۳۹	۴۴۳	۴۴۹	۴۵۷	۴۶۱	۴۶۳	۴۶۷	۴۷۹	۴۸۷	۴۹۱	۴۹۹	۵۰۳	۵۰۹	۵۲۱	۵۲۳	۵۴۱
۱۰۱–۱۲۰	۵۴۷	۵۵۷	۵۶۳	۵۶۹	۵۷۱	۵۷۷	۵۸۷	۵۹۳	۵۹۹	۶۰۱	۶۰۷	۶۱۳	۶۱۷	۶۱۹	۶۳۱	۶۴۱	۶۴۳	۶۴۷	۶۵۳	۶۵۹
۱۲۱–۱۴۰	۶۶۱	۶۷۳	۶۷۷	۶۸۳	۶۹۱	۷۰۱	۷۰۹	۷۱۹	۷۲۷	۷۳۳	۷۳۹	۷۴۳	۷۵۱	۷۵۷	۷۶۱	۷۶۹	۷۷۳	۷۸۷	۷۹۷	۸۰۹
۱۴۱–۱۶۰	۸۱۱	۸۲۱	۸۲۳	۸۲۷	۸۲۹	۸۳۹	۸۵۳	۸۵۷	۸۵۹	۸۶۳	۸۷۷	۸۸۱	۸۸۳	۸۸۷	۹۰۷	۹۱۱	۹۱۹	۹۲۹	۹۳۷	۹۴۱
۱۶۱–۱۸۰	۹۴۷	۹۵۳	۹۶۷	۹۷۱	۹۷۷	۹۸۳	۹۹۱	۹۹۷	۱۰۰۹	۱۰۱۳	۱۰۱۹	۱۰۲۱	۱۰۳۱	۱۰۳۳	۱۰۳۹	۱۰۴۹	۱۰۵۱	۱۰۶۱	۱۰۶۳	۱۰۶۹
۱۸۱–۲۰۰	۱۰۸۷	۱۰۹۱	۱۰۹۳	۱۰۹۷	۱۱۰۳	۱۱۰۹	۱۱۱۷	۱۱۲۳	۱۱۲۹	۱۱۵۱	۱۱۵۳	۱۱۶۳	۱۱۷۱	۱۱۸۱	۱۱۸۷	۱۱۹۳	۱۲۰۱	۱۲۱۳	۱۲۱۷	۱۲۲۳
۲۰۱–۲۲۰	۱۲۲۹	۱۲۳۱	۱۲۳۷	۱۲۴۹	۱۲۵۹	۱۲۷۷	۱۲۷۹	۱۲۸۳	۱۲۸۹	۱۲۹۱	۱۲۹۷	۱۳۰۱	۱۳۰۳	۱۳۰۷	۱۳۱۹	۱۳۲۱	۱۳۲۷	۱۳۶۱	۱۳۶۷	۱۳۷۳
۲۲۱–۲۴۰	۱۳۸۱	۱۳۹۹	۱۴۰۹	۱۴۲۳	۱۴۲۷	۱۴۲۹	۱۴۳۳	۱۴۳۹	۱۴۴۷	۱۴۵۱	۱۴۵۳	۱۴۵۹	۱۴۷۱	۱۴۸۱	۱۴۸۳	۱۴۸۷	۱۴۸۹	۱۴۹۳	۱۴۹۹	۱۵۱۱
۲۴۱–۲۶۰	۱۵۲۳	۱۵۳۱	۱۵۴۳	۱۵۴۹	۱۵۵۳	۱۵۵۹	۱۵۶۷	۱۵۷۱	۱۵۷۹	۱۵۸۳	۱۵۹۷	۱۶۰۱	۱۶۰۷	۱۶۰۹	۱۶۱۳	۱۶۱۹	۱۶۲۱	۱۶۲۷	۱۶۳۷	۱۶۵۷
۲۶۱–۲۸۰	۱۶۶۳	۱۶۶۷	۱۶۶۹	۱۶۹۳	۱۶۹۷	۱۶۹۹	۱۷۰۹	۱۷۲۱	۱۷۲۳	۱۷۳۳	۱۷۴۱	۱۷۴۷	۱۷۵۳	۱۷۵۹	۱۷۷۷	۱۷۸۳	۱۷۸۷	۱۷۸۹	۱۸۰۱	۱۸۱۱
۲۸۱–۳۰۰	۱۸۲۳	۱۸۳۱	۱۸۴۷	۱۸۶۱	۱۸۶۷	۱۸۷۱	۱۸۷۳	۱۸۷۷	۱۸۷۹	۱۸۸۹	۱۹۰۱	۱۹۰۷	۱۹۱۳	۱۹۳۱	۱۹۳۳	۱۹۴۹	۱۹۵۱	۱۹۷۳	۱۹۷۹	۱۹۸۷
۳۰۱–۳۲۰	۱۹۹۳	۱۹۹۷	۱۹۹۹	۲۰۰۳	۲۰۱۱	۲۰۱۷	۲۰۲۷	۲۰۲۹	۲۰۳۹	۲۰۵۳	۲۰۶۳	۲۰۶۹	۲۰۸۱	۲۰۸۳	۲۰۸۷	۲۰۸۹	۲۰۹۹	۲۱۱۱	۲۱۱۳	۲۱۲۹
۳۲۱–۳۴۰	۲۱۳۱	۲۱۳۷	۲۱۴۱	۲۱۴۳	۲۱۵۳	۲۱۶۱	۲۱۷۹	۲۲۰۳	۲۲۰۷	۲۲۱۳	۲۲۲۱	۲۲۳۷	۲۲۳۹	۲۲۴۳	۲۲۵۱	۲۲۶۷	۲۲۶۹	۲۲۷۳	۲۲۸۱	۲۲۸۷
۳۴۱–۳۶۰	۲۲۹۳	۲۲۹۷	۲۳۰۹	۲۳۱۱	۲۳۳۳	۲۳۳۹	۲۳۴۱	۲۳۴۷	۲۳۵۱	۲۳۵۷	۲۳۷۱	۲۳۷۷	۲۳۸۱	۲۳۸۳	۲۳۸۹	۲۳۹۳	۲۳۹۹	۲۴۱۱	۲۴۱۷	۲۴۲۳
۳۶۱–۳۸۰	۲۴۳۷	۲۴۴۱	۲۴۴۷	۲۴۵۹	۲۴۶۷	۲۴۷۳	۲۴۷۷	۲۵۰۳	۲۵۲۱	۲۵۳۱	۲۵۳۹	۲۵۴۳	۲۵۴۹	۲۵۵۱	۲۵۵۷	۲۵۷۹	۲۵۹۱	۲۵۹۳	۲۶۰۹	۲۶۱۷
۳۸۱–۴۰۰	۲۶۲۱	۲۶۳۳	۲۶۴۷	۲۶۵۷	۲۶۵۹	۲۶۶۳	۲۶۷۱	۲۶۷۷	۲۶۸۳	۲۶۸۷	۲۶۸۹	۲۶۹۳	۲۶۹۹	۲۷۰۷	۲۷۱۱	۲۷۱۳	۲۷۱۹	۲۷۲۹	۲۷۳۱	۲۷۴۱
۴۰۱–۴۲۰	۲۷۴۹	۲۷۵۳	۲۷۶۷	۲۷۷۷	۲۷۸۹	۲۷۹۱	۲۷۹۷	۲۸۰۱	۲۸۰۳	۲۸۱۹	۲۸۳۳	۲۸۳۷	۲۸۴۳	۲۸۵۱	۲۸۵۷	۲۸۶۱	۲۸۷۹	۲۸۸۷	۲۸۹۷	۲۹۰۳
۴۲۱–۴۴۰	۲۹۰۹	۲۹۱۷	۲۹۲۷	۲۹۳۹	۲۹۵۳	۲۹۵۷	۲۹۶۳	۲۹۶۹	۲۹۷۱	۲۹۹۹	۳۰۰۱	۳۰۱۱	۳۰۱۹	۳۰۲۳	۳۰۳۷	۳۰۴۱	۳۰۴۹	۳۰۶۱	۳۰۶۷	۳۰۷۹
۴۴۱–۴۶۰	۳۰۸۳	۳۰۸۹	۳۱۰۹	۳۱۱۹	۳۱۲۱	۳۱۳۷	۳۱۶۳	۳۱۶۷	۳۱۶۹	۳۱۸۱	۳۱۸۷	۳۱۹۱	۳۲۰۳	۳۲۰۹	۳۲۱۷	۳۲۲۱	۳۲۲۹	۳۲۵۱	۳۲۵۳	۳۲۵۷
۴۶۱–۴۸۰	۳۲۵۹	۳۲۷۱	۳۲۹۹	۳۳۰۱	۳۳۰۷	۳۳۱۳	۳۳۱۹	۳۳۲۳	۳۳۲۹	۳۳۳۱	۳۳۴۳	۳۳۴۷	۳۳۵۹	۳۳۶۱	۳۳۷۱	۳۳۷۳	۳۳۸۹	۳۳۹۱	۳۴۰۷	۳۴۱۳
۴۸۱–۵۰۰	۳۴۳۳	۳۴۴۹	۳۴۵۷	۳۴۶۱	۳۴۶۳	۳۴۶۷	۳۴۶۹	۳۴۹۱	۳۴۹۹	۳۵۱۱	۳۵۱۷	۳۵۲۷	۳۵۲۹	۳۵۳۳	۳۵۳۹	۳۵۴۱	۳۵۴۷	۳۵۵۷	۳۵۵۹	۳۵۷۱
۵۰۱–۵۲۰	۳۵۸۱	۳۵۸۳	۳۵۹۳	۳۶۰۷	۳۶۱۳	۳۶۱۷	۳۶۲۳	۳۶۳۱	۳۶۳۷	۳۶۴۳	۳۶۵۹	۳۶۷۱	۳۶۷۳	۳۶۷۷	۳۶۹۱	۳۶۹۷	۳۷۰۱	۳۷۰۹	۳۷۱۹	۳۷۲۷
۵۲۱–۵۴۰	۳۷۳۳	۳۷۳۹	۳۷۶۱	۳۷۶۷	۳۷۶۹	۳۷۷۹	۳۷۹۳	۳۷۹۷	۳۸۰۳	۳۸۲۱	۳۸۲۳	۳۸۳۳	۳۸۴۷	۳۸۵۱	۳۸۵۳	۳۸۶۳	۳۸۷۷	۳۸۸۱	۳۸۸۹	۳۹۰۷
۵۴۱–۵۶۰	۳۹۱۱	۳۹۱۷	۳۹۱۹	۳۹۲۳	۳۹۲۹	۳۹۳۱	۳۹۴۳	۳۹۴۷	۳۹۶۷	۳۹۸۹	۴۰۰۱	۴۰۰۳	۴۰۰۷	۴۰۱۳	۴۰۱۹	۴۰۲۱	۴۰۲۷	۴۰۴۹	۴۰۵۱	۴۰۵۷
۵۶۱–۵۸۰	۴۰۷۳	۴۰۷۹	۴۰۹۱	۴۰۹۳	۴۰۹۹	۴۱۱۱	۴۱۲۷	۴۱۲۹	۴۱۳۳	۴۱۳۹	۴۱۵۳	۴۱۵۷	۴۱۵۹	۴۱۷۷	۴۲۰۱	۴۲۱۱	۴۲۱۷	۴۲۱۹	۴۲۲۹	۴۲۳۱
۵۸۱–۶۰۰	۴۲۴۱	۴۲۴۳	۴۲۵۳	۴۲۵۹	۴۲۶۱	۴۲۷۱	۴۲۷۳	۴۲۸۳	۴۲۸۹	۴۲۹۷	۴۳۲۷	۴۳۳۷	۴۳۳۹	۴۳۴۹	۴۳۵۷	۴۳۶۳	۴۳۷۳	۴۳۹۱	۴۳۹۷	۴۴۰۹
۶۰۱–۶۲۰	۴۴۲۱	۴۴۲۳	۴۴۴۱	۴۴۴۷	۴۴۵۱	۴۴۵۷	۴۴۶۳	۴۴۸۱	۴۴۸۳	۴۴۹۳	۴۵۰۷	۴۵۱۳	۴۵۱۷	۴۵۱۹	۴۵۲۳	۴۵۴۷	۴۵۴۹	۴۵۶۱	۴۵۶۷	۴۵۸۳
۶۲۱–۶۴۰	۴۵۹۱	۴۵۹۷	۴۶۰۳	۴۶۲۱	۴۶۳۷	۴۶۳۹	۴۶۴۳	۴۶۴۹	۴۶۵۱	۴۶۵۷	۴۶۶۳	۴۶۷۳	۴۶۷۹	۴۶۹۱	۴۷۰۳	۴۷۲۱	۴۷۲۳	۴۷۲۹	۴۷۳۳	۴۷۵۱
۶۴۱–۶۶۰	۴۷۵۹	۴۷۸۳	۴۷۸۷	۴۷۸۹	۴۷۹۳	۴۷۹۹	۴۸۰۱	۴۸۱۳	۴۸۱۷	۴۸۳۱	۴۸۶۱	۴۸۷۱	۴۸۷۷	۴۸۸۹	۴۹۰۳	۴۹۰۹	۴۹۱۹	۴۹۳۱	۴۹۳۳	۴۹۳۷
۶۶۱–۶۸۰	۴۹۴۳	۴۹۵۱	۴۹۵۷	۴۹۶۷	۴۹۶۹	۴۹۷۳	۴۹۸۷	۴۹۹۳	۴۹۹۹	۵۰۰۳	۵۰۰۹	۵۰۱۱	۵۰۲۱	۵۰۲۳	۵۰۳۹	۵۰۵۱	۵۰۵۹	۵۰۷۷	۵۰۸۱	۵۰۸۷
۶۸۱–۷۰۰	۵۰۹۹	۵۱۰۱	۵۱۰۷	۵۱۱۳	۵۱۱۹	۵۱۴۷	۵۱۵۳	۵۱۶۷	۵۱۷۱	۵۱۷۹	۵۱۸۹	۵۱۹۷	۵۲۰۹	۵۲۲۷	۵۲۳۱	۵۲۳۳	۵۲۳۷	۵۲۶۱	۵۲۷۳	۵۲۷۹
۷۰۱–۷۲۰	۵۲۸۱	۵۲۹۷	۵۳۰۳	۵۳۰۹	۵۳۲۳	۵۳۳۳	۵۳۴۷	۵۳۵۱	۵۳۸۱	۵۳۸۷	۵۳۹۳	۵۳۹۹	۵۴۰۷	۵۴۱۳	۵۴۱۷	۵۴۱۹	۵۴۳۱	۵۴۳۷	۵۴۴۱	۵۴۴۳
۷۲۱–۷۴۰	۵۴۴۹	۵۴۷۱	۵۴۷۷	۵۴۷۹	۵۴۸۳	۵۵۰۱	۵۵۰۳	۵۵۰۷	۵۵۱۹	۵۵۲۱	۵۵۲۷	۵۵۳۱	۵۵۵۷	۵۵۶۳	۵۵۶۹	۵۵۷۳	۵۵۸۱	۵۵۹۱	۵۶۲۳	۵۶۳۹
۷۴۱–۷۶۰	۵۶۴۱	۵۶۴۷	۵۶۵۱	۵۶۵۳	۵۶۵۷	۵۶۵۹	۵۶۶۹	۵۶۸۳	۵۶۸۹	۵۶۹۳	۵۷۰۱	۵۷۱۱	۵۷۱۷	۵۷۳۷	۵۷۴۱	۵۷۴۳	۵۷۴۹	۵۷۷۹	۵۷۸۳	۵۷۹۱
۷۶۱–۷۸۰	۵۸۰۱	۵۸۰۷	۵۸۱۳	۵۸۲۱	۵۸۲۷	۵۸۳۹	۵۸۴۳	۵۸۴۹	۵۸۵۱	۵۸۵۷	۵۸۶۱	۵۸۶۷	۵۸۶۹	۵۸۷۹	۵۸۸۱	۵۸۹۷	۵۹۰۳	۵۹۲۳	۵۹۲۷	۵۹۳۹
۷۸۱–۸۰۰	۵۹۵۳	۵۹۸۱	۵۹۸۷	۶۰۰۷	۶۰۱۱	۶۰۲۹	۶۰۳۷	۶۰۴۳	۶۰۴۷	۶۰۵۳	۶۰۶۷	۶۰۷۳	۶۰۷۹	۶۰۸۹	۶۰۹۱	۶۱۰۱	۶۱۱۳	۶۱۲۱	۶۱۳۱	۶۱۳۳
۸۰۱–۸۲۰	۶۱۴۳	۶۱۵۱	۶۱۶۳	۶۱۷۳	۶۱۹۷	۶۱۹۹	۶۲۰۳	۶۲۱۱	۶۲۱۷	۶۲۲۱	۶۲۲۹	۶۲۴۷	۶۲۵۷	۶۲۶۳	۶۲۶۹	۶۲۷۱	۶۲۷۷	۶۲۸۷	۶۲۹۹	۶۳۰۱
۸۲۱–۸۴۰	۶۳۱۱	۶۳۱۷	۶۳۲۳	۶۳۲۹	۶۳۳۷	۶۳۴۳	۶۳۵۳	۶۳۵۹	۶۳۶۱	۶۳۶۷	۶۳۷۳	۶۳۷۹	۶۳۸۹	۶۳۹۷	۶۴۲۱	۶۴۲۷	۶۴۴۹	۶۴۵۱	۶۴۶۹	۶۴۷۳
۸۴۱–۸۶۰	۶۴۸۱	۶۴۹۱	۶۵۲۱	۶۵۲۹	۶۵۴۷	۶۵۵۱	۶۵۵۳	۶۵۶۳	۶۵۶۹	۶۵۷۱	۶۵۷۷	۶۵۸۱	۶۵۹۹	۶۶۰۷	۶۶۱۹	۶۶۳۷	۶۶۵۳	۶۶۵۹	۶۶۶۱	۶۶۷۳
۸۶۱–۸۸۰	۶۶۷۹	۶۶۸۹	۶۶۹۱	۶۷۰۱	۶۷۰۳	۶۷۰۹	۶۷۱۹	۶۷۳۳	۶۷۳۷	۶۷۶۱	۶۷۶۳	۶۷۷۹	۶۷۸۱	۶۷۹۱	۶۷۹۳	۶۸۰۳	۶۸۲۳	۶۸۲۷	۶۸۲۹	۶۸۳۳
۸۸۱–۹۰۰	۶۸۴۱	۶۸۵۷	۶۸۶۳	۶۸۶۹	۶۸۷۱	۶۸۸۳	۶۸۹۹	۶۹۰۷	۶۹۱۱	۶۹۱۷	۶۹۴۷	۶۹۴۹	۶۹۵۹	۶۹۶۱	۶۹۶۷	۶۹۷۱	۶۹۷۷	۶۹۸۳	۶۹۹۱	۶۹۹۷
۹۰۱–۹۲۰	۷۰۰۱	۷۰۱۳	۷۰۱۹	۷۰۲۷	۷۰۳۹	۷۰۴۳	۷۰۵۷	۷۰۶۹	۷۰۷۹	۷۱۰۳	۷۱۰۹	۷۱۲۱	۷۱۲۷	۷۱۲۹	۷۱۵۱	۷۱۵۹	۷۱۷۷	۷۱۸۷	۷۱۹۳	۷۲۰۷
۹۲۱–۹۴۰	۷۲۱۱	۷۲۱۳	۷۲۱۹	۷۲۲۹	۷۲۳۷	۷۲۴۳	۷۲۴۷	۷۲۵۳	۷۲۸۳	۷۲۹۷	۷۳۰۷	۷۳۰۹	۷۳۲۱	۷۳۳۱	۷۳۳۳	۷۳۴۹	۷۳۵۱	۷۳۶۹	۷۳۹۳	۷۴۱۱
۹۴۱–۹۶۰	۷۴۱۷	۷۴۳۳	۷۴۵۱	۷۴۵۷	۷۴۵۹	۷۴۷۷	۷۴۸۱	۷۴۸۷	۷۴۸۹	۷۴۹۹	۷۵۰۷	۷۵۱۷	۷۵۲۳	۷۵۲۹	۷۵۳۷	۷۵۴۱	۷۵۴۷	۷۵۴۹	۷۵۵۹	۷۵۶۱
۹۶۱–۹۸۰	۷۵۷۳	۷۵۷۷	۷۵۸۳	۷۵۸۹	۷۵۹۱	۷۶۰۳	۷۶۰۷	۷۶۲۱	۷۶۳۹	۷۶۴۳	۷۶۴۹	۷۶۶۹	۷۶۷۳	۷۶۸۱	۷۶۸۷	۷۶۹۱	۷۶۹۹	۷۷۰۳	۷۷۱۷	۷۷۲۳
۹۸۱–۱۰۰۰	۷۷۲۷	۷۷۴۱	۷۷۵۳	۷۷۵۷	۷۷۵۹	۷۷۸۹	۷۷۹۳	۷۸۱۷	۷۸۲۳	۷۸۲۹	۷۸۴۱	۷۸۵۳	۷۸۶۷	۷۸۷۳	۷۸۷۷	۷۸۷۹	۷۸۸۳	۷۹۰۱	۷۹۰۷	۷۹۱۹

اتحاد

اتحاد در ریاضیات (به انگلیسی: Factorization)، یک گزارۀ همواره صادق است که معمولاً برای ساده‌سازی فعالیت‌های جبری در ریاضی به‌کار می‌رود. به عبارتی بهتر؛ معادله‌ای که به ازای هر عدد حقیقی برقرار باشد اتحاد نامیده می‌شود.^[۱]

تجزیه عبارت است از شکستن یک عبارت (عدد، چندجمله‌ای یا ماتریس) به‌صورت مضربی از عبارات دیگر، به‌صورتی که حاصل‌ضرب آن‌ها عبارت اصلی را نتیجه بدهد. مثلاً عدد ۱۵ به دو عدد اول ۵ و ۳ تجزیه می‌شود و چندجمله‌ای x^۲ − ۴ به (x − ۲)(x + ۲). (برای مثال در این تجزیه از اتحاد مزدوج استفاده شده‌است) نتیجهٔ یک تجزیه همیشه حاصل‌ضربی از عبارات ساده‌تر است، و تجزیه یک چندجمله‌ای همواره یکتاست. هرچند از راه‌های مختلفی می‌توان تجزیه را انجام داد.

کاربرد اتحاد

• ساده‌سازی محاسبات اعدادی مانند۱۰۱^۲
• تجزیۀ عبارات گویا که خود در ب. م. م‌گیری و ک. م. م‌گیری کاربرد دارد.
• تجزیۀ عبارات گویا که برای حل معادلات درجۀ دو و سه و بیشتر کاربرد دارد.
• به‌دست آوردن جواب معادلات درجهٔ دو

انواع اتحاد

اتحادها بسیار زیاد هستند، اما چند اتحاد اصلی که پایهٔ اتحادهای دیگر هستند از این قرارند:

بسط دوجمله‌ای

مقالهٔ اصلی: بسط دوجمله‌ای

معادل هندسی بسط دوجمله‌ای، تا توان چهار. به عنوان مثال، مساحت مربعی به ضلع a+b برابر مجموع مساحت یک مربع به ضلع a، دو مستطیل به طول a و عرض b، و یک مربع به ضلع b است: ${\displaystyle (�+�{)}^2={�}^2+2��+{�}^2}$.

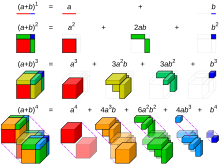
مربع دو جمله‌ای (اتحاد اول و اتحاد دوم)

مربع مجموع دو جمله‌ای

${\displaystyle (�+�{)}^2={�}^2+2��+{�}^2}$

مربع تفاضل دو جمله‌ای

${\displaystyle (�-�{)}^2={�}^2-2��+{�}^2}$

مکعب دو جمله ای

${\displaystyle (�+�{)}^3={�}^3+3{�}^2�+3�{�}^2+{�}^3}$

${\displaystyle (�-�{)}^3={�}^3-3{�}^2�+3�{�}^2-{�}^3}$

اتّحاد مربع سه جمله‌ای

${\displaystyle (�+�+�{)}^2={�}^2+{�}^2+{�}^2+2��+2��+2��}$

نکته: اتحاد مربع سه جمله‌ای برخلاف اتحادهای مربع دو جمله‌ای و مکعب دو جمله‌ای، برای تفریق کاربرد ندارد .

اتّحاد مزدوج:

${\displaystyle (�-�)(�+�)={�}^2-{�}^2}$

کاربرد اتحاد مزدوج در تجزیه عبارت های جبری:

اتّحاد مزدوج برای تجزیه کردن عبارت های جبری که به‌صورت دو جمله ی مربع کامل هستند،استفاده می شود.

نکته ۱:اتّحاد مزدوج برای تجزیه عبارت های جبری که به‌صورت مجموع دو جمله ی مربع کامل هستند،کاربرد ندارد.

نکته ۲:اتّحاد مزدوج برای تجزیه عبارت های جبری که ۳ جمله دارند،استفاده نمی شود.

اتحاد جمله مشترک

${\displaystyle (�+�)(�+�)={�}^2+(�+�)�+��}$

${\displaystyle (�+�)(�-�)={�}^2+(�-�)�-��}$

مجموع و تفاضل مکعبات دوجمله (اتحاد چاق و لاغر یا فیل و فنجان)

${\displaystyle {�}^3+{�}^3=(�+�)({�}^2-��+{�}^2),}$

${\displaystyle {�}^3-{�}^3=(�-�)({�}^2+��+{�}^2).}$

اتحاد اویلر

${\displaystyle (�+�+�)({�}^2+{�}^2+{�}^2-��-��-��)={�}^3+{�}^3+{�}^3-3���}$

اتحاد لاگرانژ

${\displaystyle ({�}^2+{�}^2)({�}^2+{�}^2)=(��-��{)}^2+(��+��{)}^2}$

بسط چندجمله‌ای نیوتن

${\displaystyle (�+�{)}^{�}=(\genfrac{}{}{0ex}{}{�}{0}){�}^{�}{�}^0+(\genfrac{}{}{0ex}{}{�}{1}){�}^{�-1}{�}^1+\cdots +(\genfrac{}{}{0ex}{}{�}{�}){�}^0{�}^{�}}$^[۲]

عدد اول

غربال گری اراتوستن الگوریتمی ساده و قدیمی برای یافتن همهٔ اعداد اول تا عدد صحیح برگزیده است. این الگوریتم پیش از غربال آتکین، که سریع‌تر و پیچیده‌تر بود، مورد استفاده قرار می‌گرفت. غربال اراتوستن را اراتوستن، ریاضیدان یونان باستان در قرن سوم پیش از میلاد ابداع کرد.

عدد اول (به انگلیسی: Prime Number)، عددی طبیعی بزرگ‌تر از ۱ است که نتوان آن را به‌صورت ضرب دو عدد طبیعی کوچک‌تر

قانون بخش پذیری

به نام خدا

الهم صل علی محمد و آل محمد

---

قانون بخش پذیری بر 13 :

... « این قانون شبیه بخش پذیری بر 7 است ؛ با این تفاوت که 13 جایگزین 7 می شود و به جای ِ کم کردن ِ 2 برابر رقم حذف شده ، 9 برابر رقم حذف شده را در هر مرحله کم می کنیم. »...

این قانون را برای بخش پذیری 6516 بر 13 به کار می بریم :

با عدد 6516 شروع می کنیم و رقم یکان آن ، 6 ، را حذف می کنیم و 9 برابر آن یعنی 54 را از عدد باقی مانده کم می کنیم : 507 = 54 -651. از آن جا که نمی توانیم تشخیص دهیم 507 بر 13 بخش پذیر است یا خیر ، روند را ادامه می دهیم .

رقم یکان ِ 507 ، یعنی 7 را حذف می کنیم و 9 برابر 7 را از عدد باقی مانده کم می کنیم :

50-63=-13

از آن جا که13- بر 13 بخش پذیر است ، عدد اصلی یعنی 6516 بر 13 بخش پذیر است ؛همچنین عدد 507 نیز بر 13 بخش پذیر خواهد بود .

قانون بخش پذیری بر 17 :

... « رقم یکان را حذف کنید و 5 برابر ِ رقم حذف شده را از عدد باقی مانده کم کنید ؛ تا زمانی که به عدد کوچکی که بتوانید تشخیص دهید آیا بر 17 بخش پذیر است یا خیر ، این عمل را تکرار کنید . »...

همان گونه که مشاهده می کنید ، این قانون شبیه بخش پذیری بر 7 و 13 است و نتایج مشابهی برای آن برقرار است .

امیدواریم این قوانین ، راهنمایی برای شما در جهت به دست آوردن قوانین بخش پذیری بر دیگر اعداد اول باشد .

جهت سامان دادن به بحث خود جدول زیر را در اختیار شما قرار می دهیم . در این جدول مشاهده می کنید که برای بخش پذیری بر هر عدد اول ، چه مضربی از رقم ِ حذف شده را از عدد باقی مانده باید کسر کنید :

در آزمون بخش پذیری بر عدد ِ اول ِ ...	چند برابرعدد حذف شده را کم کنیم ؟
7	2
11	1
13	9
17	5
19	17
23	16
29	26
31	3
37	11
41	4
43	30
47	14

بسیار جالب خواهد بود اگر شما بخواهید این جدول را کامل تر کنید . این کار احساس و درک شما را در ریاضیات افزایش می دهد . با آموختن قوانین بخش پذیری بر اعداد اول ، می توانیم قانون بخش پذیری بر اعداد مرکب ( عددی که اول نباشد ) را دقیق تر بیان کنیم :

قانون بخش پذیری بر اعداد مرکب :

...« عددی بر یک عدد ِ مرکب بخش پذیر است که بر تمام ِ مقسوم علیه های نسبت به هم اولش بخش پذیر باشد. »...

جدول زیر به شما در درک قانون بالاکمک می کند :

برای بخش پذیری بر...	عدد باید بر اعداد ... و ... بخش پذیر باشد
6	2 و 3
10	2 و 5
12	3 و 4
15	3 و 5
18	2 و 9
21	3 و 7
24	3 و 8
26	2 و 13
28	4 و 7

یاد آوری می کنیم که دو عدد نسبت به هم اول نامیده می شوند هر گاه بزرگترین مقسوم علیه مشترک آنها عدد ِ یک باشد .