
مهدی حسین پورمقدمی
دبیر ریاضی ، تبریز
مهدی حسین پورمقدمی
دبیر ریاضی ، تبریزتغیر نماد اعشاری به کسری مخصوص کسر های متناوب ساده و مرکب
یک فرمول می خواستم درباره تغیر نماد اعشاری به کسری مخصوص کسر های متناوب ساده و مرکب
فایل زیر دو فرمول قرار میدهم اولی برای متناوب ساده و دومی برای متناوب مرکب میباشد.

نماد علمی
نماد علمی، روشیست برای نوشتن اعدادی که خیلی بزرگ یا خیلی کوچکند و نمیتوان به سادگی آنها را در نماد دهدهی نوشت. این نماد به صورت دیجیتال معمولاً با e نمایش داده میشود. استفاده از نماد علمی در ماشینحسابهای علمی و توسط دانشمندان، ریاضیدانان، متخصصین سلامت و مهندسان رایج است.
در نماد علمی، کلیهٔ اعداد به شکل:
(آ ضربدر ۱۰ به توان ب) نوشته میشوند؛ که در آن توان b یک عدد صحیح، و ضریب a یک عدد حقیقی است.
| نماد دهدهی استاندارد | نماد علمی نرمالشده |
|---|---|
۳۰۰ | ۳×۱۰۲ |
۴٬۰۰۰ | ۴×۱۰۳ |
-۵۳٬۰۰۰ | −۵٫۳×۱۰۴ |
۶٬۷۲۰٬۰۰۰٬۰۰۰ | ۶٫۷۲×۱۰۹ |
۰٫۰۰۰ ۰۰۰ ۰۰۷ ۵۱ | ۷٫۵۱×۱۰−۹ |
کایت(هندسه)
| هندسه |
|---|
 |
| فهرست هندسهدانان |

در هندسه اقلیدسی یک کایت(kite) چهارضلعی محدّبی است که دو ضلع مجاور برابر داشته باشد. یعنی برخلاف متوازیالأضلاع که دو ضلع روبهروی برابر دارد. این چهارضلعی مانند بادبادکی است که در آسمان پرواز میکند و به همین دلیل اینگونه نامگذاری شدهاست.
حالت ویژه
- اگر تمام چهار لبهٔ یک کایت درازای یکسان داشته باشند (چندضلعی متساوی الاضلاع)، آنگاه آن کایت، خود، یک لوزی است.
- اگر تمام زاویههای یک کایت با هم برابر باشد، آنگاه آن کایت، خود، یک مربع است.
- در میان همهٔ چهارضلعیها تنها شکلی که بیشترین نسبت پیرامون به قطر را دارد، یک کایت با قطرهای متساوی است که زاویههای π/۳ و ۵π/۱۲ و ۵π/۶ و ۵π/۱۲ داشته باشد.[۱]
مساحت
در همهٔ بادبادکها قطرها بر هم عمودند و یکی دیگری را دو نیم میکنند و البته نیمساز زاویههای روبرو هم هست. پس عمود منصف قطر دیگر است.[۲] مساحت یک کایت برابر است با نصف حاصل ضرب دو قطر آن:
پس اگر هر یک از قطرهای کایت طولی برابر با p و q داشته باشند و مساحت کایت را K بنامیم، آنگاه:
اگر طول ضلعهای روبروی کایت را داشته باشیم که به ترتیب a و b باشد و θ زاویهٔ میان دو ضلع نابرابر، آنگاه مساحت چنین بدست میآید:
یادآوری میشود با کشیدن دو قطر کایت دو مثلث متساویالساقین پدید میآید در نتیجه چون زاویههای دو ساق مثلث با هم برابر اند پس زاویههای روبرو در کایت هم با هم برابر اند.[۲]
ذوزنقه سه گونه است
شکل زیر یک ذوزنقه را نشان میدهد و همانطور که میبینیم، فقط دو ضلع آن موازی هستند. روی این ذوزنقه، قاعده، ساق، قطر و ارتفاع مشخص شدهاند. در ادامه، این اصطلاحات را معرفی میکنیم.
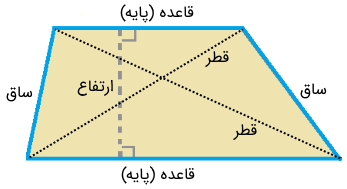
- قاعده: دو ضلعی از ذوزنقه که موازی هم هستند، قاعده (پایه) نام دارند.
- ساق: غیر از دو قاعده، ذوزنقه دو ضلع دیگر نیز دارد که موازی نیستند و به آنها ساق میگوییم.
- ارتفاع: به کوتاهترین فاصله بین دو قاعده هر ذوزنقه ارتفاع میگوییم. ارتفاع ذوزنقه بر هر دو قاعده آن عمود است.
- قطر: قطر ذوزنقه پارهخطی است که دو رأس زوایای مقابل را به هم وصل میکند. هر ذوزنقه دو قطر دارد.
ذوزنقهها را میتوان به سه دسته تقسیم کرد: ذوزنقه متساوی الساقین، ذوزنقه قائم الزاویه و ذوزنقه مختلف الاضلاع.
۱. ذوزنقه قائمالزاویه
۲. ذوزنقه متساویالساقین
ذوزنقه متساویالساقین به ذوزنقهای گفته میشود که ساقهای آن هماندازه باشند. میتوان نشان داد که یک ذوزنقه متساویالساقین است اگر و تنها اگر: دو پایهٔ آن همنهشت باشند. زاویههای بالایی (و پایینی) پایهها با هم همنهشت باشند.
۳. ذوزنقه مختلفالاضلاع
ذوزنقه متساویالساقین
| ذوزنقه متساویالساقین | |
|---|---|
 یک ذوزنقه متساویالساقین و محور تقارن آن | |
| نوع | چهارضلعی، ذوزنقه |
| اضلاع و رئوس | ۴ |
| گروه تقارن | Dih2، [ ]، (*)، مرتبه ۲ |
| چندضلعی دوگان | بادبادک |
| خواص | کوژ، دایره محیطی |
ذوزنقه متساویالساقین به ذوزنقهای گفته میشود که ساقهای آن هماندازه باشند. میتوان نشان داد که یک ذوزنقه متساویالساقین است اگر و تنها اگر:
- دو پایهٔ آن همنهشت باشند.
- زاویههای بالایی (و پایینی) پایهها با هم همنهشت باشند.
- قطرهای ذوزنقه همنهشت باشند.
وجود هر یک از این شرطها در یک ذوزنقه متضمن دیگری است.[۱]
ذوزنقههای متساویالساقین چهارضلعی محاطی هستند.[۲]
زاویه های رو به رو با هم برابر هستند.
زاویه های بالا و پایین مکمل یکدیگرند.
مربع
یک چهارضلعی محدب یک مربع است اگر و تنها اگر یکی از شرطهای زیر را داشته باشد:[۲][۳]
- یک راستگوشه با دو ضلع مجاور برابر.
- یک چهارضلعی با چهار لبهٔ برابر (ضلع برابر) و چهار زاویهٔ راست.
- یک متوازیالأضلاع با یک زاویهٔ راست و دو ضلع مجاور برابر.
- یک لوزی با یک زاویهٔ راست.
- یک لوزی با چهار زاویهٔ برابر.
- یک چهارضلعی که قطرهای آن با هم برابرند و بر یکدیگر عمودند و همدیگر را به دو نیم تقسیم میکنند (عمودمنصفند) مانند یک لوزی با قطرهای برابر.
- یک مستطیل که طول چهار ضلع آن با هم برابر است.


