مهدی حسین پورمقدمی
دبیر ریاضی ، تبریز
مهدی حسین پورمقدمی
دبیر ریاضی ، تبریزدرباره من
پر بازدیدها
سوالات نهایی دوازدهم ریاضی مهدی حسین پورمقدمی سوالات نهایی دوازدهم ریاضیات نهم مهدی مقدمی سوالات نهایی دوازدهم انسانی ریاضی و آمار (3) حسابان 2 ریاضی نهم استدلال عقلانی شهریور 1402 سوالات ریاضی هماهنگ استان آذربای ریاضیات نهم نهایی ریاضی نهم تضمینی riazyamoz سوالات نهایی دوازدهم تجربی دوازدهم ریاضی ریاضیات گسسته نهایی دوازدهم ریاضی و آمار 3 خرداد99 ریاضی و آمار (3) دوازدهم انسانی دوازدهم انسانی ریاضی 3 دوازدهم تجربی تبریزجدیدترین یادداشتها
همه- بارم بندی امتحان ریاضی نهم
- بارم بندی ریاضی پایه هشتم
- آموزش آنلاین ریاضیات
- نمونه سوال ریاضی هشتم فصلهای 1 تا 5
- شروع به فعالیت کانال در آپارات
- شروع کلاسهای آمادگی برای امتحانات خرداد
- آزمون ورودی پایه دهم مدارس نمونه دولتی استان آذربایجان شرقی
- آزمون آنلاین ریاضی نهم
- عیدتان مبارک دانش اموزان عزیز
- شروع کلاسهای آموزشی ریاضی
بایگانی
- فروردین 1404 6
- فروردین 1403 3
- اسفند 1402 1
- دی 1402 1
- آذر 1402 37
- آبان 1402 1
- مهر 1402 15
- شهریور 1402 18
- مرداد 1402 11
- تیر 1402 3
- خرداد 1402 3
- اردیبهشت 1402 1
- فروردین 1402 3
- دی 1401 10
- آبان 1401 1
- مرداد 1401 2
- خرداد 1401 2
- فروردین 1401 3
- بهمن 1400 2
- دی 1400 1
- آذر 1400 1
- آبان 1400 3
- شهریور 1400 2
- مرداد 1400 2
- اسفند 1399 1
- بهمن 1399 3
- دی 1399 4
- آذر 1399 2
- آبان 1399 8
- شهریور 1399 3
- مرداد 1399 3
- تیر 1399 9
- خرداد 1399 3
- فروردین 1399 1
- بهمن 1398 5
- دی 1398 1
- آبان 1398 4
- شهریور 1398 30
- مرداد 1398 5
- آذر 1397 4
- خرداد 1397 1
- اردیبهشت 1397 5
- فروردین 1397 2
تقویم
فروردین 1404| ش | ی | د | س | چ | پ | ج |
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
جستجو
ضرب صلیبی
ضرب صلیبی
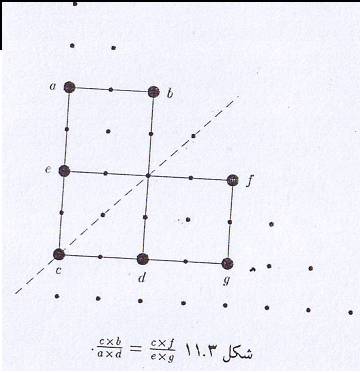
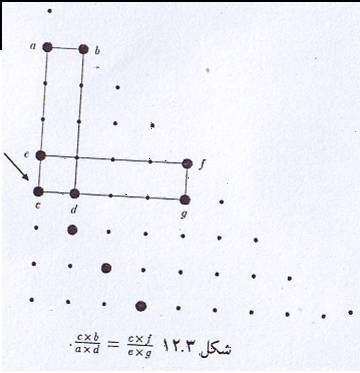
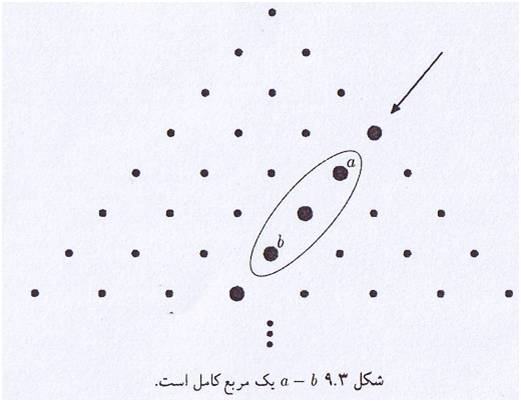
در اینجا مستطیلهایی را به صورت قائم الزاویه و افقی در داخل مثلث خیام در نظر میگیریم. رئوس این مستطیلها که بر روی درایههای این مثلث واقع شدهاند در اینجا رابطهای بر حسب درایههای واقع بر رئوس این مستطیل به دست می آوریم. نکته جالب این است که با لغزاندن مستطیل به نحوی که نقطهٔ cدر طول قطر (در امتداد پیکان) جابهجا شود
همواره نسبت (a*d)/(c*b)یک مقدار ثابت خواهد بود
ویژگی چوب چوگان در مثلث خیام پاسکال
ویژگی چوب چوگان
تساوی زیر را در نظر بگیرید.
اگر هر کدام از عناصر دو طرف تساوی را به صورت نقاط هندسی در نظر بگیرید

اگر طول چوب چوگان را kدر نظر بگیریم (رابطه بالا را تعمیم دهید)

ویژگی هندسی فانگ مثلث خیام پاسکال
ویژگی هندسی فانگ
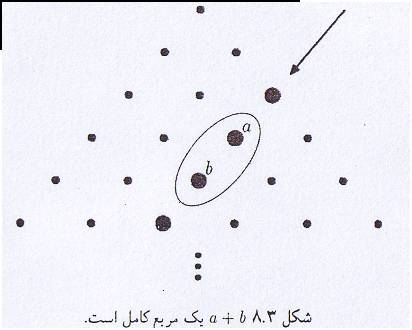
ایا دو عدد در مثلث پاسکال میتوان یافت که مجموع یا تفاضلشان مربع کامل باشد؟ عناصر واقع در قطر ۳، اعداد مثلثی هستندو نیز مجموع ۲ عدد مثلثی متوالی یک مربع کامل است. اگر Tnنشان دهنده nامین عدد مثلثی باشد. داریم:
Tn+Tn+1=n2
واین نتیجه میدهد.
برای تفریق داریم
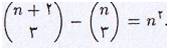
دنبالهٔ فیبوناتچی و مثلث خیام پاسکال
دنبالهٔ فیبوناتچی
اگر قطرها را با شیب بیشتر انتخاب کنیم. داریم:
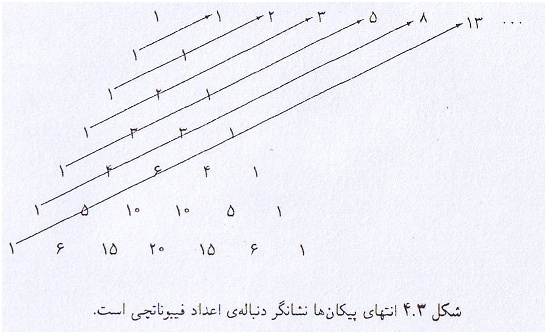
مجموعه اعداد روی قطرها دنبالهٔ :
… و۱۳و۸و۵و۳و۱و۱
تشکیل میدهد. در این دنباله جمله اول ودوم ۱ است بقیه جملات جمع دو جمله قبلی اش میشوند
F1=F2=1 Fn+۲=Fn+1+Fn
اثبات این خاصیت به وسیله مثلث به راحتی قابل مشاهده است. اگر شیب قطرهای فیبوناچی را بیشتر کنیم. به تعمیمی از این دنباله دست خواهیم یافت
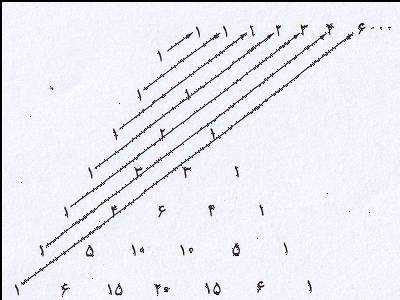
اگر ان را با Gn نمایش دهیم داریم
G1=G2=G3=1 Gn+۲=Gn+1+Gn-1
تعمیمهای مختلف از دنباله فیبوناچی داریم.
دنبالهٔ اعداد مصور و مثلث خیام پاسکال
دنبالهٔ اعداد مصور
در مثلث پاسکال قطر از اعداد طبیعی، قطر ۲ از اعداد مثلثی و قطر۳ از اعداد ۴وجهی تشکیل شدهاند.
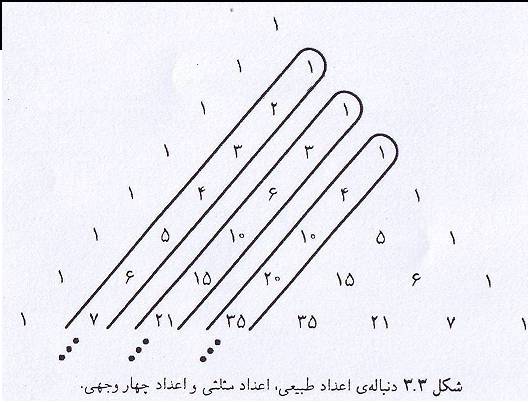
با نگاه به قطرهای مثلث ملاحظه میشود که هر عدد مثلثی مجموع چند عدد طبیعی وهر عدد ۴ وجهی مجموع چند عدد مثلثی است. بهطور کلی میتوان گفت که قطر kام از اعداد مصور kبعدی تشکیل شدهاند که به صورت (c(n,kمیباشد. در ضمن داریم: