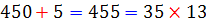قاعده بخشپذیری بر 13 :
عددی بر13 بخش پذیر است که اگر 4 برابر رقم یکان آن را با عددی که از حذف یکان به دست آمده جمع کنیم، حاصل بر13 بخش پذیر باشد.(در صورت لزوم این عمل را چندین بار تکرار می کنیم تا به نتیجه برسیم.) مثال: 13÷689
104 = 36 + 68 = 9 × 4 + 68
چون26 بر 13 قابل قسمت است پس 689 بر 13 قابل قسمت است. 26 = 4 × 4 + 10
*نکته:
اگر یک عدد 3 رقمی را دو بار کنار هم بنویسیم تا یک عدد 6 رقمی به دست آید؛ این عدد 6 رقمی حتماً بر اعداد 7 و 11 و 13 بخشپذیر خواهد بود. مثال: 256 عدد256256 هم بر 7 و هم بر 11 و هم بر 13 قابل قسمت است.
125 = 13 ÷ 11 ÷ 7 ÷ 125125 125125 = 13× 11× 7× 125
قاعده بخشپذیری بر 14 : 14 = 7 × 2
اعدادی که هم بر 2 و هم بر 7 بخشپذیر باشند؛ بر 14 نیز بخشپذیرند. یا اعداد زوجی که بر 7 بخشپذیر باشند.
مثال: 140 ، 28 ، 560 ، 714210280003500490
قاعده بخشپذیری بر 15 : 15 = 5 × 3
اعدادی که هم بر 3 و هم بر 5 بخشپذیر باشند؛ بر 15 نیز بخشپذیرند. مثال: 45 ، 270 ، 555 ، 97215
قاعده بخشپذیری بر 16 :
عددی بر 16 بخشپذیر است که چهار رقم سمت راست آن صفر یا بر 16 بخشپذیر باشد.
مثال: 10000 ، 50000 ، 3750016 ، 96870032، 235641632
قاعده بخشپذیری بر 17 :
عددی بر17 بخش پذیر است که اگر 5 برابر رقم یکان آن را از عددی که از حذف یکان به دست آمده کم کنیم، حاصل بر۷ بخش پذیر باشد.(در صورت لزوم این عمل را چندین بار تکرار می کنیم تا به نتیجه برسیم.)
مثال: 17 × 153 0 = 3 × 5 – 15
قاعده بخشپذیری بر 18 :
اعدادی که هم بر 2 و هم بر 9 بخشپذیر باشند؛ بر 18 نیز بخشپذیرند.یا اعداد زوجی که بر 9 قابل قسمت اند.
مثال: 36 ، 2574 ، 720000 ، 1234567890
قاعده بخشپذیری بر 19 :
عددی بر19 بخش پذیر است که اگر 2 برابر رقم یکان آن را با عددی که از حذف یکان به دست آمده جمع کنیم، حاصل بر19 بخش پذیر باشد.(در صورت لزوم این عمل را چندین بار تکرار می کنیم تا به نتیجه برسیم.) مثال: 19÷285
38 = 28 + 5 × 2
قاعده بخشپذیری بر 20 :
اعدادی که هم بر 4 و هم بر 5 بخشپذیر باشند؛ بر 20 نیز بخشپذیرند.
اعدادی بر 20 قابل قسمت هستند که یکان آنها صفر و رقم دهگان آنها زوج باشد. مثال: 40 ، 7380 ، 35700
قاعده بخشپذیری بر 21 :
اعدادی که هم بر 3 و هم بر 7 بخشپذیر باشند؛ بر 21 نیز بخشپذیرند. مثال: 42 ، 84 ، 105، 214200
قاعده بخشپذیری بر 22 :
اعدادی که هم بر 2 و هم بر 11 بخشپذیر باشند؛ بر 22 نیز بخشپذیرند.یا اعداد زوجی که بر 11 قابلقسمتند.
مثال:44 ، 66 ، 88 ، 286 ، 594 ، 110 ، 374374
قاعده بخشپذیری بر 23 :
عددی بر23 بخش پذیر است که اگر 7 برابر رقم یکان آن را با عددی که از حذف یکان به دست آمده جمع کنیم، حاصل بر23 بخش پذیر باشد.(در صورت لزوم این عمل را چندین بار تکرار می کنیم تا به نتیجه برسیم.)
مثال: 23 ÷ 138 69 = 8 × 7 + 13
قاعده بخشپذیری بر 24 :
اعدادی که هم بر 3 و هم بر 8 بخشپذیر باشند؛ بر 24 نیز بخشپذیرند. مثال: 48 ، 72 ، 888000 ، 3000
قاعده بخشپذیری بر 25 :
اعدادی بر 25 بخشپذیرند که دو رقم سمت راست آنها بر 25 بخشپذیر باشد.
اعدادی بر 25 بخشپذیرند که دو رقم سمت راست آنها 00 ، 25 ، 50 و یا 75 باشد.
مثال : 300 ، 13425 ، 9852150 ، 321475
برای تعیین باقیماندهی تقسیم یک عدد بر 25 بزرگترین مضرب ممکن 25 را از دو رقم سمت راست عدد کم میکنیم.
مثال : 25 ÷ 473283 چون 8 = 75 – 83 پس تقسیم مربوطه 8 تا باقیمانده دارد.
قاعده بخشپذیری بر 50 :
اعدادی بر 50 بخشپذیرند که دو رقم سمت راست آنها بر 50 بخشپذیر باشد.
اعدادی بر 25 بخشپذیرند که دو رقم سمت راست آنها 00 و یا 50 باشد.
مثال : 300 ، 123450 ، 7900000
اگر دو رقم سمت راست عددی کمتر از 50 بود آن دو رقم همان باقیمانده ی تقسیم میباشد.
اگر دو رقم سمت راست عددی بزرگتر از 50 بود؛ 50 را از آن کم می کنیم.
مثال: در تقسیم 50 ÷ 12342 باقیمانده 42 میباشد. در تقسیم 584290 باقیمانده ی تقسیم 50-90 یعنی 40 میباشد.
قاعده بخشپذیری بر 75 :
اعدادی که هم بر 3 و هم بر 25 بخشپذیر باشند؛ بر 75 نیز بخشپذیرند. مثال: 150 ، 225 ، 75000
قاعده بخشپذیری بر 99 :
اعدادی که هم بر 9 و هم بر 11 بخشپذیر باشند؛ بر 99 نیز بخشپذیرند. مثال : 495 ، 3960 ، 369369
قاعده بخشپذیری بر 100 :
اعدادی که هم بر 4 و هم بر 25 بخشپذیر باشند؛ بر 100 نیز بخشپذیرند. یا اعدادی که دو رقم سمت راست آنها صفر باشد. مثال: 700 ، 12340000
دو رقم سمت راست هر عدد باقیمانده ی آن عدد بر 100 خواهد بود. مثال: باقیمانده ی 100÷ 234578 عدد 78 میباشد.
نکته: با استفاده از قاعده بخشپذیری بر 10 و 100 میتوان به قاعده ی بخشپذیری بر 1000 ، 100000 ، دست یافت.
نکته : اگر در تقسیمی مقسوم بر مقسوم علیه بخشپذیر باشد؛ مقسوم بر تمامی مقسوم علیهای این مقسوم علیه نیز بخشپذیر است. مثلاً 100 بر 50 ، 25 ، 20 ، 10 ، 5 ، 4 و 2 قابل قسمت است و چون 200 بر 100 بخشپذیر است؛
پس 200 بر50 ، 25 ، 20 ، 10 ، 5 ، 4 و 2 نیز قابل قسمت است.
قاعده بخشپذیری بر 13 :
